1.非参数化概率密度的估计
对于未知概率密度函数的估计方法,其核心思想是:一个向量x落在区域R中的概率可表示为:
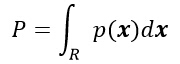
其中,P是概率密度函数p(x)的平滑版本,因此可以通过计算P来估计概率密度函数p(x),假设n个样本x1,x2,…,xn,是根据概率密度函数p(x)独立同分布的抽取得到,这样,有k个样本落在区域R中的概率服从以下分布:
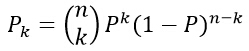
其中k的期望值为:
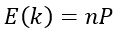
- k的分布在均值附近有着非常显著的波峰,因此若样本个数n足够大时,使用k/n作为概率P的一个估计将非常准确。假设p(x)是连续的,且区域R足够小,则有:
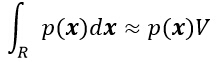
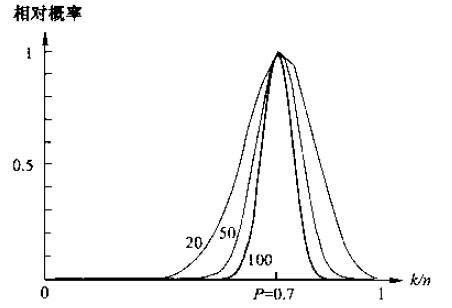
- 如下图所示,以上公式产生一个特定值的相对概率,当n趋近于无穷大时,曲线的形状逼近一个δ函数,该函数即是真实的概率。公式中的V是区域R所包含的体积。综上所述,可以得到关于概率密度函数p(x)的估计为:
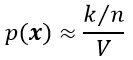
- 在实际中,为了估计x处的概率密度函数,需要构造包含点x的区域R1,R2,…,Rn。第一个区域使用1个样本,第二个区域使用2个样本,以此类推。记Vn为Rn的体积。kn为落在区间Rn中的样本个数,而pn (x)表示为对p(x)的第n次估计:
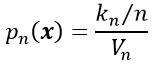
- 欲满足pn(x)收敛:pn(x)→p(x),需要满足以下三个条件:
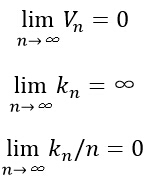
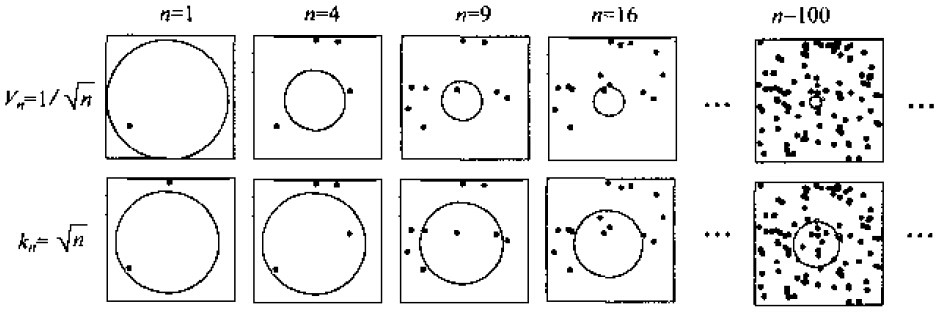
- 有两种经常采用的获得这种区域序列的途径,如下图所示。其中“Parzen窗方法”就是根据某一个确定的体积函数,比如Vn=1/√n来逐渐收缩一个给定的初始区间。这就要求随机变量kn和kn/n能够保证pn (x)能收敛到p(x)。第二种“k-近邻法”则是先确定kn为n的某个函数,如kn=√n。这样,体积需要逐渐生长,直到最后能包含进x的kn个相邻点。
2.Parzen窗估计法
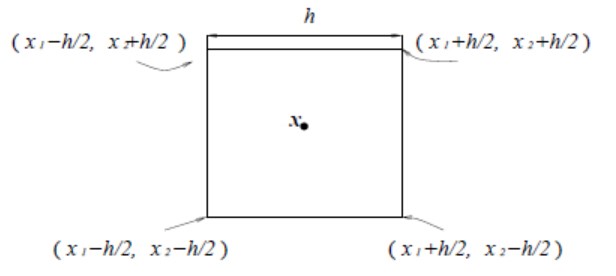
- 已知测试样本数据x1,x2,…,xn,在不利用有关数据分布的先验知识,对数据分布不附加任何假定的前提下,假设R是以x为中心的超立方体,h为这个超立方体的边长,对于二维情况,方形中有面积V=h^2,在三维情况中立方体体积V=h^3,如下图所示。
- 根据以下公式,表示x是否落入超立方体区域中:
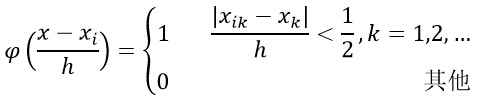
- 估计它的概率分布:
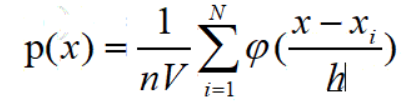
- 其中n为样本数量,h为选择的窗的长度,φ(.)为核函数,通常采用矩形窗和高斯窗。
3.k最近邻估计
- 在Parzen算法中,窗函数的选择往往是个需要权衡的问题,k-最近邻算法提供了一种解决方法,是一种非常经典的非参数估计法。基本思路是:已知训练样本数据x1,x2,…,xn而估计p(x),以点x为中心,不断扩大体积Vn,直到区域内包含k个样本点为止,其中k是关于n的某一个特定函数,这些样本被称为点x的k个最近邻点。
- 当涉及到邻点时,通常需要计算观测点间的距离或其他的相似性度量,这些度量能够根据自变量得出。这里我们选用最常见的距离度量方法:欧几里德距离。
- 最简单的情况是当k=1的情况,这时我们发现观测点就是最近的(最近邻)。一个显著的事实是:这是简单的、直观的、有力的分类方法,尤其当我们的训练集中观测点的数目n很大的时候。可以证明,k最近邻估计的误分概率不高于当知道每个类的精确概率密度函数时误分概率的两倍。
matlab实现Parzen和k最近邻估计
Parzen窗方法研究
- 采用3类满足正太分布的样本数据(w1,w2,w3)作为训练样本,编写程序,使用Parzen 窗估计方法对一个任意的测试样本点x 进行分类。对分类器的训练则使用(w1,w2,w3)的三维数据。同时修改窗口h的值,多次实验。用于分类的样本点为x1(0.5,1.0,0.0),x2(0.31,1.51,-0.50),x3(-0.3,0.44,-0.1)。
- 训练样本数据(w1,w2,w3)分别为:
w1 = [ 0.28 1.31 -6.2
0.07 0.58 -0.78
1.54 2.01 -1.63
-0.44 1.18 -4.32
-0.81 0.21 5.73
1.52 3.16 2.77
2.20 2.42 -0.19
0.91 1.94 6.21
0.65 1.93 4.38
-0.26 0.82 -0.96];
W2 = [0.011 1.03 -0.21
1.27 1.28 0.08
0.13 3.12 0.16
-0.21 1.23 -0.11
-2.18 1.39 -0.19
0.34 1.96 -0.16
-1.38 0.94 0.45
-0.12 0.82 0.17
-1.44 2.31 0.14
0.26 1.94 0.08];
W3 = [ 1.36 2.17 0.14
1.41 1.45 -0.38
1.22 0.99 0.69
2.46 2.19 1.31
0.68 0.79 0.87
2.51 3.22 1.35
0.60 2.44 0.92
0.64 0.13 0.97
0.85 0.58 0.99
0.66 0.51 0.88]; - h=0.1时:
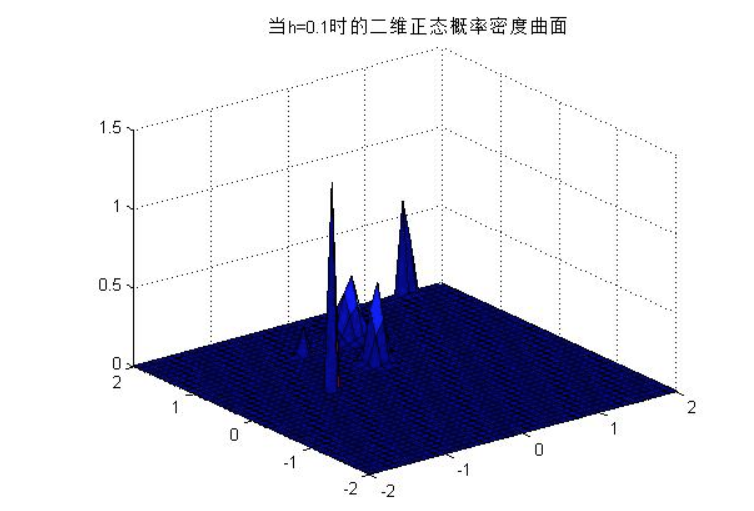
- h=0.5时:
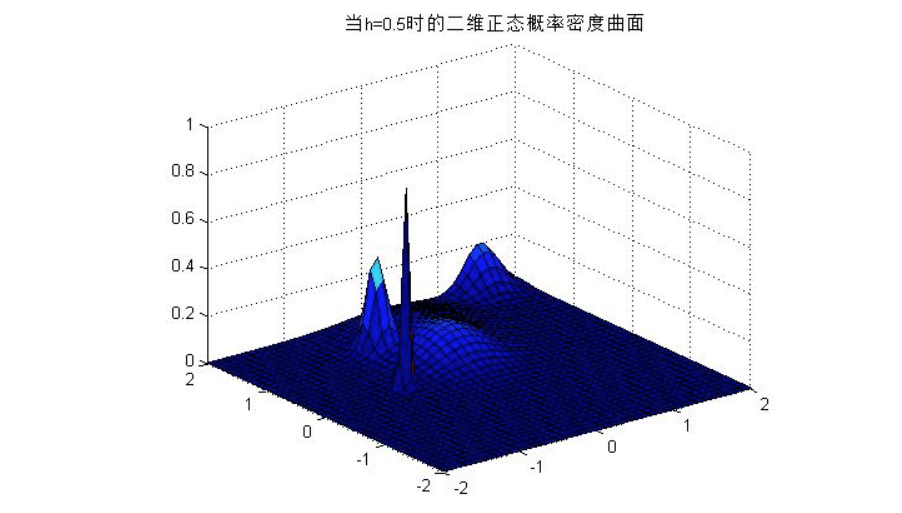
- h=1时:
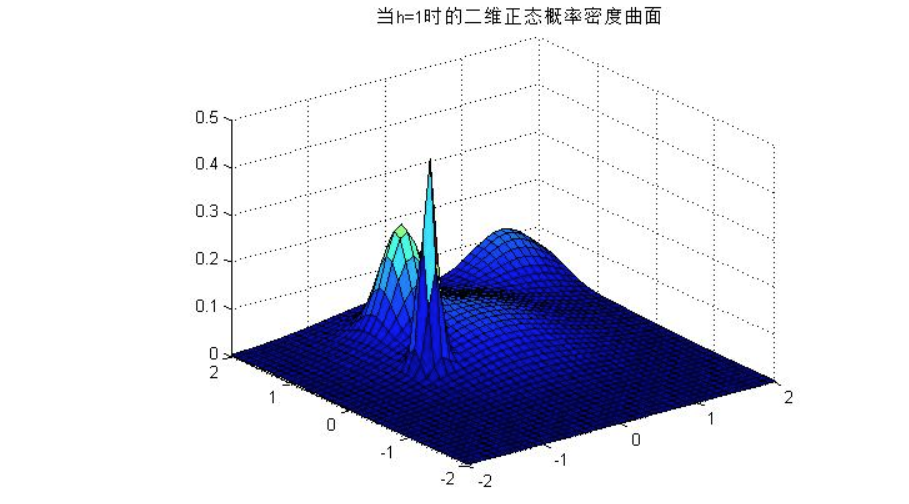
K最近邻方法研究
- 采用3类满足正太分布的样本数据(w1,w2,w3)作为训练样本,为了使实验更具有说服力,我们令训练样本数据的个数分别为10、20、30、40个样本,进行4次实验,其中w1的均值为0.2,方差为0.2,w2的均值为0,方差为0.1,w3的均值为0.1,方差为0.1。实验的训练样本都是程序随机生成的,我们将在实验结果分析的最后给出每次实验的训练样本数据。
源码
clear;
close all;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Parzen窗估计和k最近邻估计
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% w1(:,:,1) = .2+sqrt(0.2)*randn(20,[3,1]); %均值为0.2,方差为0.2的训练样本
% disp(w1(:,:,1));
% w1(:,:,2) = 0+sqrt(0.2)*randn(20,[3,.1]); %均值为0,方差为0.1的训练样本
% disp(w1(:,:,2));
% w1(:,:,3) = .1+sqrt(0.3)*randn(20,[3,0]); %均值为0.1,方差为0.1的训练样本
% disp(w1(:,:,2));
w1(:,:,1) = [ 0.28 1.31 -6.2;...
0.07 0.58 -0.78;...
1.54 2.01 -1.63;...
-0.44 1.18 -4.32;...
-0.81 0.21 5.73;...
1.52 3.16 2.77;...
2.20 2.42 -0.19;...
0.91 1.94 6.21;...
0.65 1.93 4.38;...
-0.26 0.82 -0.96];
w1(:,:,2) = [0.011 1.03 -0.21;...
1.27 1.28 0.08;...
0.13 3.12 0.16;...
-0.21 1.23 -0.11;...
-2.18 1.39 -0.19;...
0.34 1.96 -0.16;...
-1.38 0.94 0.45;...
-0.12 0.82 0.17;...
-1.44 2.31 0.14;...
0.26 1.94 0.08];
w1(:,:,3) = [ 1.36 2.17 0.14;...
1.41 1.45 -0.38;...
1.22 0.99 0.69;...
2.46 2.19 1.31;...
0.68 0.79 0.87;...
2.51 3.22 1.35;...
0.60 2.44 0.92;...
0.64 0.13 0.97;...
0.85 0.58 0.99;...
0.66 0.51 0.88];
x(1,:) = [0.5 1 0];
x(2,:) = [0.31 1.51 -0.5];
x(3,:) = [-0.3 0.44 -0.1];
h = 1; % 重要参数
p1 = Parzen(w1,x(1,:),h);
%num1 = find(p1 == max(p1));
p2 = Parzen(w1,x(2,:),h);
%num2 = find(p2 == max(p2));
p3 = Parzen(w1,x(3,:),h);
%num3 = find(p3 == max(p3));
disp(['点:[',num2str(x(1,:)),']落在三个类别的概率分别为:',num2str(p1)]);
disp(['点:[',num2str(x(2,:)),']落在三个类别的概率分别为:',num2str(p2)]);
disp(['点:[',num2str(x(3,:)),']落在三个类别的概率分别为:',num2str(p3)]);
% 给定三类二维样本,画出二维正态概率密度曲面图验证h的作用
num =1; % 第num类的二维正态概率密度曲面图,取值为1,2,3
draw(w2,h,num);
str1='当h=';str2=num2str(h);str3='时的二维正态概率密度曲面';
SC = [str1,str2,str3];
title(SC);
% k近邻算法设计的分类器
% x1和y1为测试样本
x1 = [-0.91,0.32,0.48];
x2 = [0.14,0.72, 1.1];
x3 = [-0.81,0.61,-0.38];
% x1 = [-0.41,0.82,0.88];
% x2 = [0.14,0.72, 4.1];
% x3 = [-0.81,0.61,-0.38];
w = w1;
%w = w1(:,1,3);
k = 2;
kNearestNeighbor(w,k,x1);
kNearestNeighbor(w,k,x2);
kNearestNeighbor(w,k,x3);
% Parzen窗算法
% w:c类训练样本
% x:测试样本
% h:参数
% 输出p:测试样本x落在每个类的概率
function p = Parzen(w,x,h)
[xt,yt,zt] = size(w);
p = zeros(1,zt);
for i = 1:zt
hn = h;
for j = 1:xt
hn = hn / sqrt(j);
p(i) = p(i) + exp(-(x - w(j,:,i))*(x - w(j,:,i))'/ (2 * power(hn,2))) / (hn * sqrt(2*3.14));
end
p(i) = p(i) / xt;
end
% k-最近邻算法
% w:c类训练样本
% x:测试样本
% k:参数
function p = kNearestNeighbor(w,k,x)
% w = [w(:,:,1);w(:,:,2);w(:,:,3)];
[xt,yt,zt] = size(w);
wt = [];%zeros(xt*zt, yt);
if nargin==2 %判断输入变量的个数
p = zeros(1,zt);
for i = 1:xt
for j = 1:xt
dist(j,i) = norm(wt(i,:) - wt(j,:)); % 计算向量范数(dist:欧式距离加权函数)
end
t(:,i) = sort(dist(:,i));
m(:,i) = find(dist(:,i) <= t(k+1,i)); % 找到k个最近邻的编号
end
end
if nargin==3 %判断输入变量的个数
for q = 1:zt
wt = [wt; w(:,:,q)]; % 把3个训练样本放到一个矩阵中
[xt,yt] = size(wt);
end
for i = 1:xt
dist(i) = norm(x - wt(i,:));
end
t = sort(dist); % 欧氏距离排序
[a,b] = size(t);
m = find(dist <= t(k+1)); % 找到k个最近邻样本的编号,存到向量m中
num1 = length(find(m>0 & m<11));
num2 = length(find(m>10 & m<21));
num3 = length(find(m>20 & m<31));
if yt == 3
plot3(w(:,1,1),w(:,2,1),w(:,3,1), 'r.');
hold on;
grid on;
plot3(w(:,1,2),w(:,2,2),w(:,3,2), 'g.');
plot3(w(:,1,3),w(:,2,3),w(:,3,3), 'b.');
if (num1 > num2) || (num1 > num3)
plot3(x(1,1),x(1,2),x(1,3), 'ro');
disp(['点:[',num2str(x),']属于第一类']);
elseif (num2 > num1) || (num2 > num3)
plot3(x(1,1),x(1,2),x(1,3), 'go');
disp(['点:[',num2str(x),']属于第二类']);
elseif (num3 > num1) || (num3 > num2)
plot3(x(1,1),x(1,2),x(1,3), 'bo');
disp(['点:[',num2str(x),']属于第三类']);
else
disp('无法分类');
end
end
if yt == 2
plot(w(:,1,1),w(:,2,1), 'r.');
hold on;
grid on;
plot(w(:,1,2),w(:,2,2), 'g.');
plot(w(:,1,3),w(:,2,3), 'b.');
if (num1 > num2) || (num1 > num3)
plot(x(1,1),x(1,2), 'ro');
disp(['点:[',num2str(x),']属于第一类']);
elseif (num2 > num1) || (num2 > num3)
plot(x(1,1),x(1,2), 'go');
disp(['点:[',num2str(x),']属于第二类']);
elseif (num3 > num1) || (num3 > num2)
plot(x(1,1),x(1,2), 'bo');
disp(['点:[',num2str(x),']属于第三类']);
else
disp('无法分类');
end
end
end
title('k-最近邻分类器');
legend('第一类数据',...
'第二类数据',...
'第三类数据',...
'测试样本点');
参考书籍:《模式分类》作者:RichardO.Duda,PeterE.Hart,DavidG.Stork