数据结构之二叉树的四种遍历方法

二叉树的遍历

我用下图的树为例，做树的遍历：

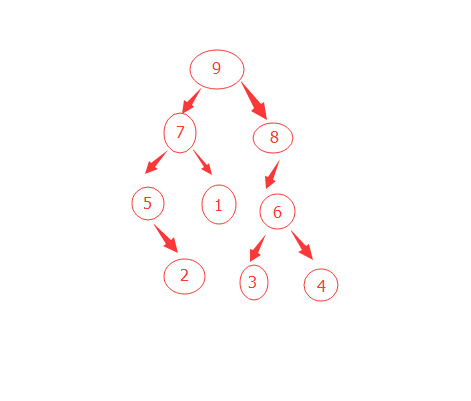
树节点的定义：

public class TreeNode {
		int val = 0;
	    TreeNode left = null;
	    TreeNode right = null;
	    public TreeNode(int val) {
	        this.val = val;
	    }
		public TreeNode(int val, TreeNode left, TreeNode right) {
			super();
			this.val = val;
			this.left = left;
			this.right = right;
		}
	}

树的结构的代码实现：

public static void main(String[] args) {
	   TreeNode e = new TreeNode(1);
	   TreeNode g = new TreeNode(2);
	   TreeNode h = new TreeNode(3);
	   TreeNode i = new TreeNode(4);
	   TreeNode d = new TreeNode(5,null,g);
	   TreeNode f = new TreeNode(6,h,i); 
	   TreeNode b = new TreeNode(7,d,e);
	   TreeNode c = new TreeNode(8,f,null);
	   TreeNode root = new TreeNode(9,b,c);
}

中序遍历

先处理左子树，然后处理当前节点，再处理右子树。
对于一颗二叉查找树，所有的信息都是有序排列的，中序遍历可以是信息有序输出，且运行时间为O（n）。

递归实现中序遍历：

public static void printTree(TreeNode t){
			if(t!=null){
				printTree(t.left);
				System.out.print(t.val+" ");
				printTree(t.right);
			}
		}

输出结果：
```
5 2 7 1 9 3 6 4 8 
```

后序遍历

先处理左右子树，然后再处理当前节点，运行时间为O（n）。

递归实现后序遍历：

public static void printTree(TreeNode t){
	if(t!=null){
		printTree(t.left);
		printTree(t.right);
		System.out.print(t.val+" ");
	}
}

输出结果：
```
2 5 1 7 3 4 6 8 9 
```

先序遍历

先处理当前节点，在处理左右子树。

递归实现先序遍历：

   public static void printTree(TreeNode t){
	if(t!=null){
		System.out.print(t.val+" ");
		printTree(t.left);
		printTree(t.right);
	}
}

输出结果：
```
9 7 5 2 1 8 6 3 4 
```

有没有觉得树的先序，中序，后序遍历都非常简单，递归三行代码就搞定了。好吧，下边厉害的要来了

层序遍历

层序遍历:所有深度为D的节点要在深度为D+1的节点之前进行处理，层序遍历与其他类型的遍历不同的地方在于它不是递归地执行的，它用到队列，而不使用递归所默示的栈。
算法思想：
1. 定义节点 TreeNode lastNode指向当前行最有节点，TreeNode nlastNode指向下一行最右节点。
2. 利用队列，首先将根节点入队,再循环里出队,并将其子节点入队,定义TreeNode tmpNode节点指向当前出队列的节点，当tmpNode==lastNode时，代表当前行遍历结束，输出换行，再令lastNode=nlastNode，nlastNode在子节点入队列时指向下一行最右节点。循环直到对列为空就行。

层序遍历代码：

package Tree;
	import java.util.ArrayList;
	import java.util.LinkedList;
	import java.util.List;
	import java.util.Queue;
	/*
	 * 层序遍历
	 * 
	 */
	public class TreePrinter1 {
		 public static int[][] printTree(TreeNode root) {
			 List< List<Integer> > list = new ArrayList< List<Integer> >();
			 list.add(new ArrayList<Integer>());
			 Queue<TreeNode> queue = new LinkedList<TreeNode>();
		        queue.add(root);
		        TreeNode lastNode = root;	// 当前行最右节点
		        TreeNode nlastNode = root;	// 下一行最右节点
		        TreeNode tmpNode = null; 
		        int hight = 0;				// 树的高度
		        while(!queue.isEmpty()){
		        	tmpNode = queue.poll();
		        	if(tmpNode!=null){
		        		list.get(hight).add(tmpNode.val);
		        	}
		        	if(tmpNode.left!=null){
		        		queue.add(tmpNode.left);
		        		nlastNode = tmpNode.left;
		        	}
		        	if(tmpNode.right!=null){
		        		queue.add(tmpNode.right);
		        		nlastNode = tmpNode.right;
		        	}
		        	if(tmpNode == lastNode){
		        		lastNode = nlastNode;
		        		hight++;
		        		list.add(new ArrayList<Integer>());
		        	}
		        }
		        int[][] data = new int[list.size()][];
		        for(int i=0;i<list.size();i++){
		        	for(int j=0;j<list.get(i).size();j++){
		        		data[i][j] = list.get(i).get(j);
		        	}
		        }		        
			return data;
		 }
		 public static void main(String[] args) {
			   TreeNode e = new TreeNode(1);
			   TreeNode g = new TreeNode(2);
			   TreeNode h = new TreeNode(3);
			   TreeNode i = new TreeNode(4);
			   TreeNode d = new TreeNode(5,null,g);
			   TreeNode f = new TreeNode(6,h,i);
			   TreeNode b = new TreeNode(7,d,e);
			   TreeNode c = new TreeNode(8,f,null);
			   TreeNode root = new TreeNode(9,b,c);
			   int[][] data  =TreePrinter.printTree(root);
			   for(int s=0;s<data.length;s++){
				   for(int j=0;j<data[s].length;j++){
					   System.out.print(data[s][j]+" ");
				   }
				   System.out.println();
			   }
		}
	}

输出结果：

二叉树的遍历

中序遍历

后序遍历

先序遍历

层序遍历

往期精彩文章