- 当我们训练网络的时候,通常会出现如下两种情况:
- 第一种情况:训练数据表现不好,这种时候通常可以使用新的激活函数,或者调整学习率。
- 第二种情况:训练数据表现的很好,但是测试数据的表现很差,这个时候可以提前终止、数据正则化和Dropout的方法来改善情况。

- 不一定网络越深,performance越好。
- 接下来我们先讨论针对以上两种情况,具体如何改善:
- 对于训练数据表现不好时,用新的激活函数(New Activation function),再讨论**调整学习率(Adaptive Learning Rate)**。
- 训练数据表现的很好,但是测试数据的表现很差时:提前终止、数据正则化和Dropout的方法来改善情况。
第一种情况之激活函数
梯度消失问题
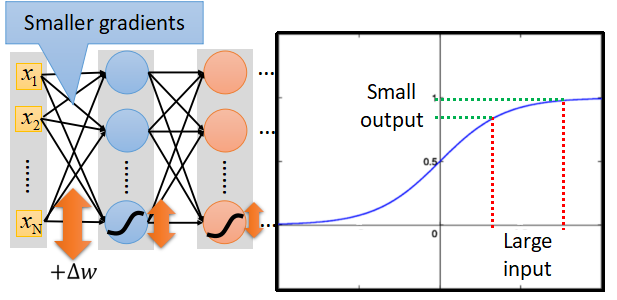
- 网络在做梯度下降时,如果我们用sigmoid作为激活函数,在接近输出的地方梯度很大,学习速度快,通过反向传播,在接近出入层的地方,梯度会变得很缓,学习效率很慢。这就是梯度消失的问题。
- 因为sigmoid在接近0和1的地方会突然变得很缓慢。如图:
- 为了解决这个问题,我们引入其它激活函数。
整流线性单元(ReLU)
- 很自然的,我们会想到能不能引入一个变换均匀的激活函数,这样就能减缓梯度消失的问题了。于是我们引入了ReLU,它的函数图像如下:
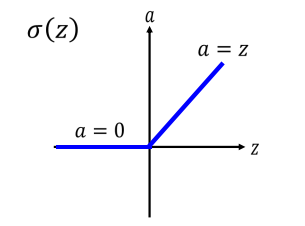
- 小于0的部分函数值为0,大于0的部分函数为
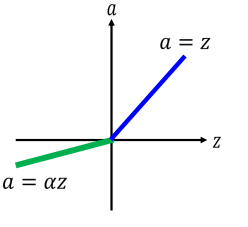
a=z。 - ReLU的变种,有人觉得z值小于0的部分函数值为0,这个还是不好,没有梯度了。于是引入ReLU的变种。令z<0的部分函数值为
a = αz,其中α 也可以根据gradient descent学习出来,这样激活函数就变得更加合理了,可以在一定程度上减少训练时间。函数图像如下:
Maxout
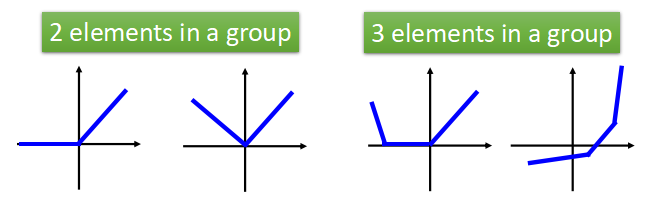
- 顾名思义,输出最大值,使用这种激活函数时,需要两个及以上结点组成一组,从下图中我们可以看出Maxout是如何工作的。
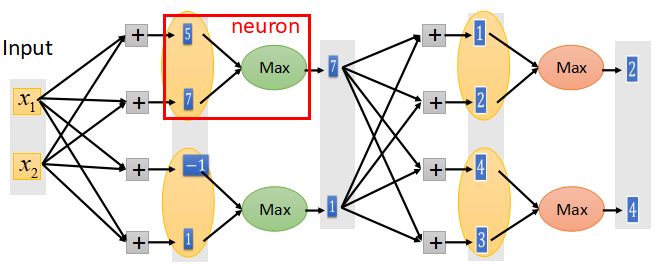
- Maxout是可学习的激活函数,它可以是任何分段线性凸函数。有几段取决于每一组中元素的个数。
第一种情况之学习率
- 前面在讲梯度下降的时候讲到了
Adagrad的方法,就是将每个参数的学习率除以其先前导数的均方根当作步长,在深度神经网络中,要介绍一种与Adagrad类似的学习率调整方法:RMSProp。
RMSProp
- 使用
RMSProp方法的权值更新公式如下:
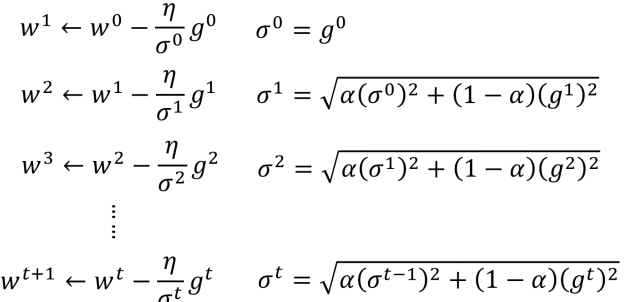
- 可以通过调整
α使得下一次的权值调整是受当前梯度倒数gt的影响都一些还是受前面的调整多一些。如果α接近0,则受当前梯度倒数gt影响多一些。 - 而且
α的值还可以通过gradient descen的方法学习出来。 - 但是这种方法很难找到全局最优值,通常在遇到局部最优点的时候就停止了。
动量(Momentum)
- 现实生活中,当一个球从高处滚落下来,在遇到平坦处和低谷处时,由于惯性的原因有可能还会继续滚动,直到到达全局最低点的位置。因此在机器学习中,通过学习率更新权值时,能不能也引入一个
惯性,使迭代到达局部最优时,还有有一个动量继续向前,直到到达全局最优呢? - 基于这个想法,接下来开始
Momentum方法:使移动的方向不仅基于当前求导的方向,还要参考上一次移动的方向。参数的更新过程如下:

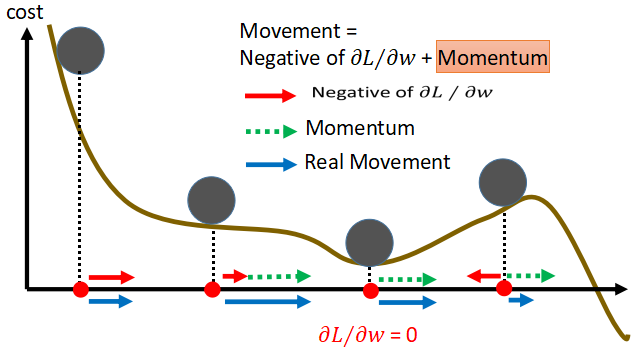
- 加入了动量之后权值更行的过程中运动轨迹如下,在遇到平坦处和低谷时,由于受到上一次方向的影响,还会继续向前。
- Adam:
RMSProp + Momentum称为Adam。
第二种情况
Early Stopping
- 网络在训练的过程中,可能训练的时间越长,对
Training set的performance就越好,但是用训练时间很长得到的参数作用于Testing set时,有可能并不会得到预期中的好结果,反而提前结束训练得到的参数作用于Testing set能得到相对满意的结果。

- 所以我们在训练时,有时需要提前结束,至于到底什么时候结束,我们也不清楚,这个时候,验证集的作用就体现出来了。
- 在
Training set分出一部分数据用来做Validation set,当获得的参数在Validation set取得好结果的时候,就停止训练,再将参数作用于Testing set。
正则化(Regularization)
- 权值更新公式如下:
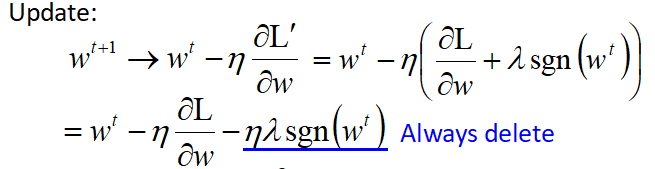
- 其中sgn(x)时符号函数,x为正数时值为1,x值为负数时,值为-1,x为0时,值为0.
Dropout
- 在每次训练之前,都摘掉p%和神经元,如下图所示:
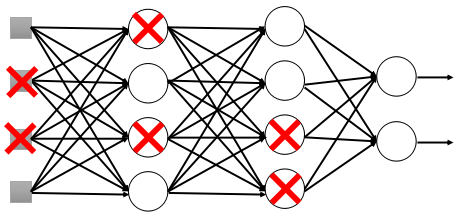
- 这样训练没循环一次我们都是使用新的网络结构在训练。如果训练时神经元的摘除率为p%,则最后所哦于权值都乘以1-p%。
- 假设
dropout rate为50%,如果通过训练得到的权值为w=1,则最后令w=0.5作用于Testing set。
