机器学习之线性回归案例研究

前言

• 在机器学习中，回归则是根据样本研究其两个（或多个）变量之间的依存关系，是对于其趋势的一个分析预测。
  • 比如说根据当前的股市行情预测接下来的股票走势；
  • 根据消费者过去的消费习惯预测他将来会购买某物；

样例分析

• 根据当前pokemon的cp值以及其他属性，预测它进化之后的cp值。

  Step1：create Model（创建模型）

• 建立回归方程，假设方程为线性的：

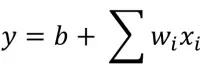
• 其中xi为pokemon的特征（feature），wi:权重(weight);b:偏差(bias)；y为预测的升级之后pokemon的Cp值。
• 假设现在只考虑pokemon当前cp值这一个feature，于是方程可以变成：

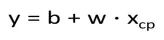
• 现在问题变成如何找到偏差b与权值w使得预测出来的y接近真实值y，首先想到的是穷举负无穷到正无穷之间的数，从而找到最优的b和w.这显然不可能。于是，我们想能不能从已有的真实数据集上学习出我们想要的偏差b与权值w？

  step2:loss function（损失函数）

• 假设我们已经知道了，10组pokemon的cp值以及升级后的cp值，根据回归方程，我们定义损失函数L。

• 损失函数L的结果等于真实值减去方程预测出来的值，上图红线部分为预测值，显然L是w和b的函数，现在我们的目标变成寻找使损失函数L最小的w和b。

  Step 3: Gradient Descent（梯度下降）

• 这回我们当然不能再用穷举法求w和b了。我们可以用一个稍微高级一点的方法了，叫做梯度下降法，我们先以单个变量讲解度下降法，先只考虑W。

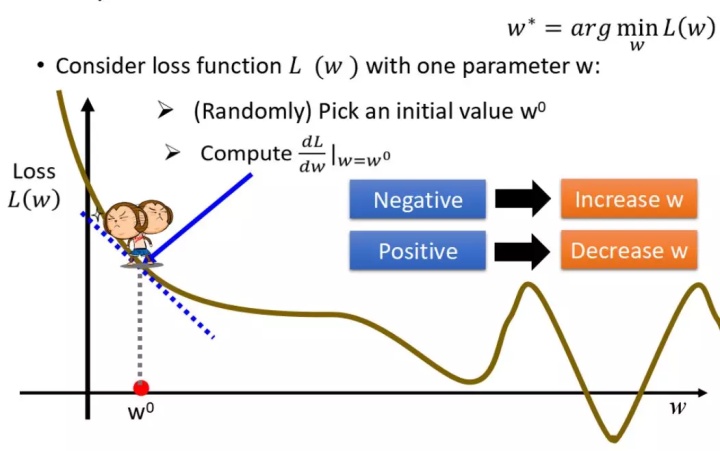
• 图为损失函数L的曲线，只需要找到使L最小的W值，在图中可以很容易的看出，L的最小值在谷底取得，但是我们不知道此时W取何值，所以需要先随机初始化w，再沿着曲线下降的方向慢慢调整w,直到L取到最小值，此时的w就为我们求的w.
• 曲线下降，我们很容易想到该点的斜率，即斜率小于0，则曲线下降，可以加大w，斜率大于0，则曲线上升，减少w。
• 斜率就是在该点求导咯，于是w可以按如下公式调整：

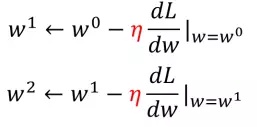
• 这样我们就能相对快一点找到使L最小的W了。
• 刚刚只是考虑W一个参数，考虑w和b两个参数的话，就让L同时对w和l求偏导，再按偏导符号调整就可以了。如图：

• 如下公式即位损失函数L的梯度：

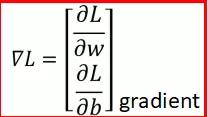
over fitting（过拟合）

• 当我们令回归方程为一次时，即方程形式如下：

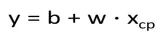
• 用梯度下降的方法求出b和w,再去预测pokemon的测试数据时，平均误差为35.当我们将回归方程设为2次时：

• 用梯度下降法求出W和b,再去预测pokemon的测试数据时，平均误差为18.于是猜想是不是回归方程的次数越高，对测试数据的预测就越准确呢？

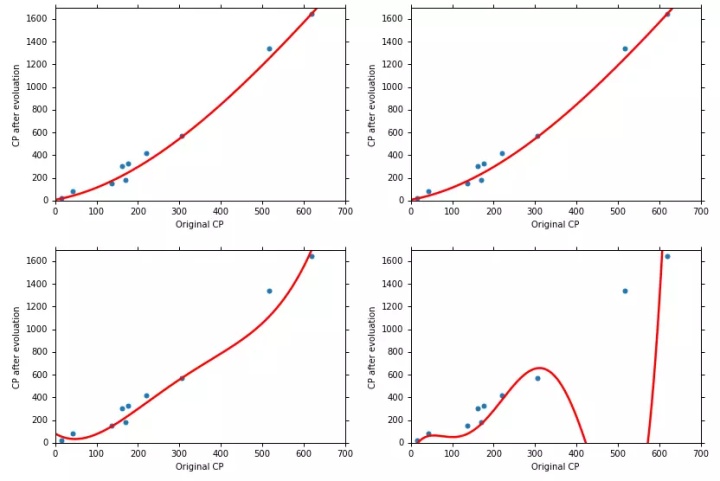
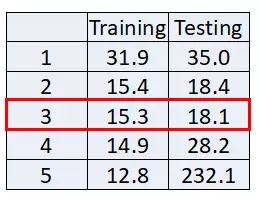
• 上图分别是当回归方程是2、3、4、5次时，回归方程预测的曲线图，最后一张是对training data 和 testing data的误差，由图可知，虽然回归方程越复杂，对训练数据效果越好，但是对测试数据可能会更差，这就是over fiting。