Matlab实现Graph cut
最大流最小割
最大流最小割最开始从图论的概念中引来,讲述一个带有起点与终点并且具有边权值的网络图中,如何进行边的切割,把这个网络图分成独立的两个部分(或者多个部分),使得这个切割中被切割的边的权值之和最小。比如现在有一个网络图如下:
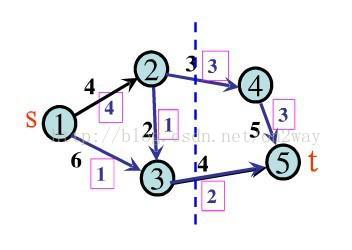
那么要把这个图分割成两部分,如上虚线就是一种切割方式,消耗的权值3+4=7,当然,切割的方式有很多种,不同的切割对应不同的切割边权值,而最大流最小割就是找到一种切割方式使得切割的边的权值之和最小。
最大流最小割应用到图像分割
图像简单来说就是矩阵,对于灰度图像,那么就是一般的二维矩阵,矩阵中值得大小就是改点的灰度值,那么图像分割问题就是寻找到图像的边界,而边界肯定在两个像素值差别很大的邻域间,如果把两个邻域间的像素值的差定义为该领域的边权值,那么分割问题就转化为如何切割这些边的问题了,这样的模型就和上述的最大流最小割对应上了。有点、有边、有边权值,那么就可以运用上述理论分割图像了。
图割理论
理论化介绍都是直观上的对图像的操作,而实际变成现实的时候是要事先转化到一维或者直接调用相应的函数才能对二维图像进行操作。先介绍一维图割操作,在介绍二维如何转为一维。
源点s与汇点t
- 如下图所示的由五个点site组成的一维情况,假设最终我们要分成两类,那么就把这两类认为是源点s与汇点t好了,那么一次类推,如果要分成多个类的话,就可以加相应的节点s或者t表示他们的类就可以了。
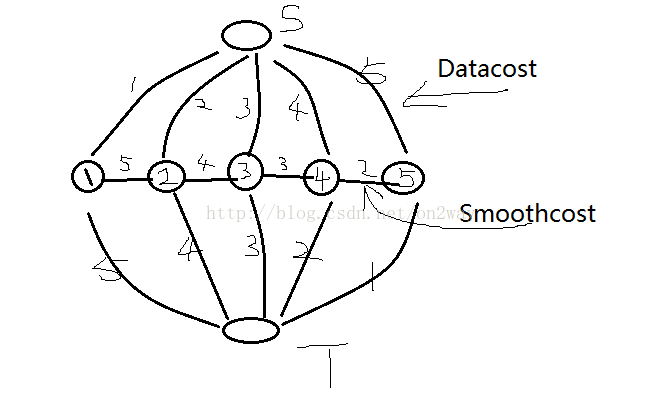
- 如下图所示的由五个点site组成的一维情况,假设最终我们要分成两类,那么就把这两类认为是源点s与汇点t好了,那么一次类推,如果要分成多个类的话,就可以加相应的节点s或者t表示他们的类就可以了。
点与点之间的权值Smoothcost
从下图上也可以看出在这个一维点与点之间相连接的权值就是Smoothcost项,图中为了简化只是画出了相邻的两个点之间有一条线连接,也就是他们之间存在着权值(这里图为一个无向图,也就是权值是没有方向之分的),正常情况下,可能每两个点之间都可能存在着联系,比如如果点1与点3之间,你也可以看成他们是连接的,只不过他们之间的权值为0而已。这也是matlab里面表示这一项点与点权值的时候用一个n*n维矩阵的原因(n为点数),像这里,如果权值的大小如上图所示定义的话,那么这个图的Smoothcost项的权值矩阵可以表示:
0 5 0 0 0
5 0 4 0 0
0 4 0 3 0
0 0 3 0 2
0 0 0 2 0
点与源汇点(类点)之间的权值Datacost
除了上述的Smoothcost项之外,图割理论中还有一种项就是Datacost,表示的是各个点到源汇点(类点)之间的权值大小,这一项的权值同样对于分割至关重要。比如我们知道点1与点2属于s,其他点属于t的话,那么最终优化的结果就是1-s,2-s之间的权值可能很大,3-s,4-s,5-s之间的权值都很小,这对分割最后的形式很重要。Datacost也可以用矩阵表示,用c表示类的话(这里只有s与t那么c为2),n表示点的个数的话,那么Datacost可以表示为一个c*n的矩阵了:
1 2 3 4 5
5 4 3 2 1
最大流最小割的实现过程
关于具体怎么解最大流最小割的方法有很多种,假设在上述Smoothcost和Datacost都定死的情况下,具体有以下几种方法实现:
- Ford-Fulkerson方法(增大路径最大流算法)
- Edmonds-Karp(EK)算法实现
- Dinic算法
- SAP算法(最短路径增广算法)
- Preflow push method(预流-推进最大流方法)
里面有详细的c语言代码,可供详细研究实现这个的过程。
graph cut之图割工具箱GCO3.0
有了前面的介绍,我们大致了解了分割的过程,下面下载GCO3.0的源码,下载地址:http://vision.csd.uwo.ca/code/,在这里找到对应的内容即可。
解压源码包之后里面会有一些c编写的代码以及另一个matlab版文件夹,如图:
matlab文件夹中有很多.m文件和一个C文件
注意在使用这些代码时,matlab文件夹和外面的c编写的代码文件相对位置不要发生改变,因为在程序的执行过程中.m文件会调用.cpp文件。
我们主要用到的是matlab文件中提供的函数对图像进行分割,在正式分割之前我们需要先自己编写几个辅助函数:
Datacost1函数:用来计算点与类的权值datacost,代码如下:
function datacost = Datacost1(img,ctrs)
[m,n] = size(img);
num_lables = size(ctrs,1);
totalsizes = m*n;
datacost = zeros(totalsizes,num_lables);
for i = 1:totalsizes
Ip = double(img(i));
for j = 1:num_lables
datacost(i,j) = (Ip - ctrs(j)).^2; %计算datacost项
end
end
neighbours1函数:计算点与点之间的权值neighbours,代码如下:
%%-------------------
% 每个点的灰度作为特征
%%-------------------
function Neighbours = neighbours1(img)
[m,n] = size(img);
totalsizes = m*n;
var_img = var(img(:)); %图像方差
%% 选择neigh=4四连通计算权值,neigh=8八连通计算权值
neigh = 4;
%%
if neigh == 4
%构建索引向量--生成距离的稀疏矩阵
i1 = (1:totalsizes-m)';
j1 = i1+m;
for i = 1:n
i2_tem(:,i) = (i-1)*m + (1:m-1)';
end
i2 = i2_tem(:);
j2 = i2+1;
%对应边的值
ans1 = exp(-(img(i1(:))-img(j1(:))).^2/(2*var_img));
ans2 = exp(-(img(i2(:))-img(j2(:))).^2/(2*var_img));
%组合相应的向量:x位置,y位置,权值(注意必须都是列向量)
all = [[i1;i2],[j1;j2],[ans1;ans2]];
else
%构建索引向量--生成距离的稀疏矩阵
i1 = (1:totalsizes-m)'; %正右权值
j1 = i1+m;
for i = 1:n %正下权值
i2_tem(:,i) = (i-1)*m + (1:m-1)';
end
i2 = i2_tem(:);
j2 = i2+1;
for i = 1:n-1 %斜下权值
i3_tem(:,i) = (i-1)*m + (1:m-1)';
end
i3 = i3_tem(:);
j3 = i3+n+1;
i4 = i3+1; %斜上权值
j4 = i3+m;
%对应边的值
ans1 = exp(-(img(i1(:))-img(j1(:))).^2/(2*var_img));
ans2 = exp(-(img(i2(:))-img(j2(:))).^2/(2*var_img));
ans3 = exp(-(img(i3(:))-img(j3(:))).^2/(2*var_img));
ans4 = exp(-(img(i4(:))-img(j4(:))).^2/(2*var_img));
%组合相应的向量:x位置,y位置,权值(注意必须都是列向量)
all = [[i1;i2;i3;i4],[j1;j2;j3;j4],[ans1;ans2;ans3;ans4]];
end
%matlab函数生成稀疏矩阵(这么做的速度最快) %----------------
neighb = spconvert(all);
neighb(totalsizes,totalsizes) = 0;
Neighbours = neighb;
end
有了上述的工具函数之后,我们就可以编程调用这些函数实现图像分割了, 下面给出综合起来的主程序:
clc;
clear;
img = imread('b_04_95.jpg');
img = double(img);
% 定义分类数Numlables
Numlables = 2;
% 定义Potts模型参数K
Potts_K = 1500;
[m,n] = size(img);
totalsizes =n*m;
%k-means预分类找到中心与分类
%init_lable预分类,列向量; ctrs-类中心灰度值值
[init_lable,ctrs] = kmeans(img(:),Numlables); %img通过索引转化为列向量可用
ctrs_new = zeros(Numlables,1);
% 生成目标体
h = GCO_Create(totalsizes,Numlables);
%设置初始标签
GCO_SetLabeling(h,init_lable);
%设置datacost项
datacost = Datacost1(img,ctrs);
datacost = datacost';
GCO_SetDataCost(h,datacost);
%设置smoothcost
%不设置的时候默认使用potts模型
SmoothCost = eye(Numlables);
SmoothCost = 1 - SmoothCost;
GCO_SetSmoothCost(h,SmoothCost);
%设置neighbors项
Neighbours = Potts_K*neighbours1(img);
GCO_SetNeighbors(h,Neighbours);
%显示输出结果
GCO_SetVerbosity(h,2);
%类标签运算顺序
GCO_SetLabelOrder(h,randperm(Numlables));
%膨胀算法
GCO_Expansion(h);
%获得该标签lables
Labeling = GCO_GetLabeling(h); %列向量
% 释放内存
GCO_Delete(h);
%显示graph cut分类
for i = 1:length(Labeling)
img1(i) = ctrs(Labeling(i));
end
img1 = reshape(img1,m,n);
%绘制分割图
figure;
%原图像
subplot(1,2,1);imshow(img,[]);
title('原始图像');
%显示graph cut分类
subplot(1,2,2);imshow(img1,[]);
title(['Potts模型参数:',num2str(Potts_K)]);
因为涉及到matlab和C语言的混合编程,因此在执行上述代码之前需要先安装好C语言编译器,通常安装了VS软件就没什么问题了,然后在执行时可能会出现一个如下的错误:
Error using mex (line 206)
Unable to complete successfully.
- 此时我们安装mex编译器,在matlab的命令行输入:
mex -setup
根据提示选择
y和需要的编译器就可以了,程序再执行就会出现结果了。如题所示:另外可以通过调节
Potts_K参数的值,以实现不同的效果。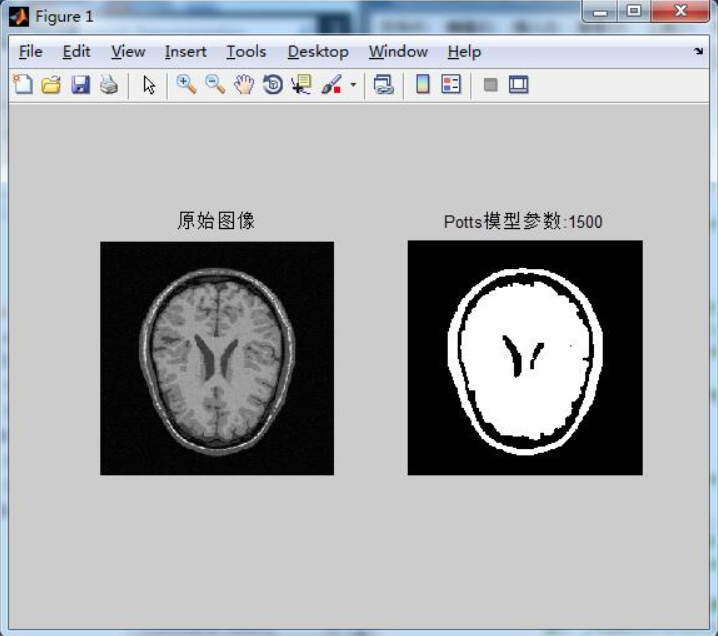
参考博客:
