流行学习(Manifold Learning)
- 流行学习(
Manifold Learning)是机器学习、模式识别中的一种方法,再维数简约方面具有广泛的应用。他的主要思想是将高维的数据映射到低维,使该低维的能够放映高维数据的某些本质特征。 - 流行学习的前提使有一种假设,假设某些高维数据实际是一种低维的流行结构嵌入再高维空间中。流行学习的目的是将其映射回低维空间中,揭示其本质。
- 下图可以特别形象的解释流行学习:
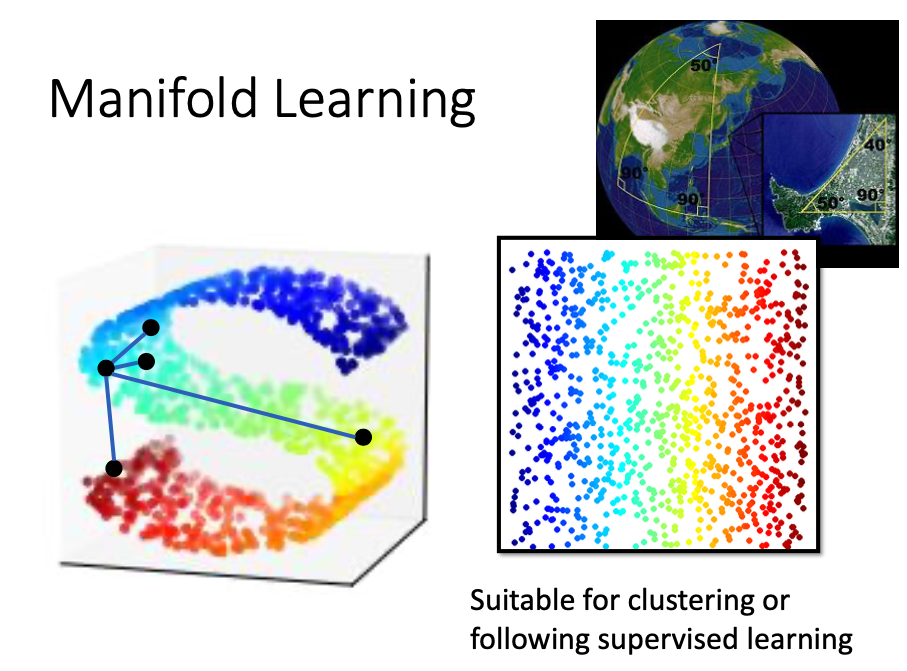
- 因为只有在同一维中,欧式距离才具有比较的意义,在上面这样的高维空间中式欧式距离并不能将不同的点进行很好的区分。
- 在流行学习中认为上面这种情况实际上是将低维数据强行塞进了一个高维空间,所以我们应该将这个高维数据摊平,以便于后面的聚类或者接下来的有监督学习。更常用的应用是将它们可视化。
- 接下来将依次介绍如下几种常用的将高维数据进行降维的方法:
- 局部线性嵌入(Locally Linear Embedding,LLE).
- 拉普拉斯特征映射(Laplacian Eigenmaps).
- t分布随机邻居嵌入(T-distributed Stochastic Neighbor Embedding,t-SNE).
局部线性嵌入(Locally Linear Embedding,LLE)
- 如下图所示,首先对于某个数据点
xi选择它附近若干个点xj,用wij代表xi和xj之间的关系,通过最小化下面的式子获得对应的权重:
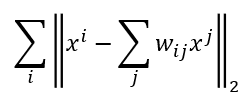
- 在这个式子中,对于某个数据点
xi认为它可以通过它周围的所有点的线性组合进行标识,令所有的点xj的线性表示与实际点xi的距离最小,得到点之间的权重wij,然后用得到的权重wij进行降维。
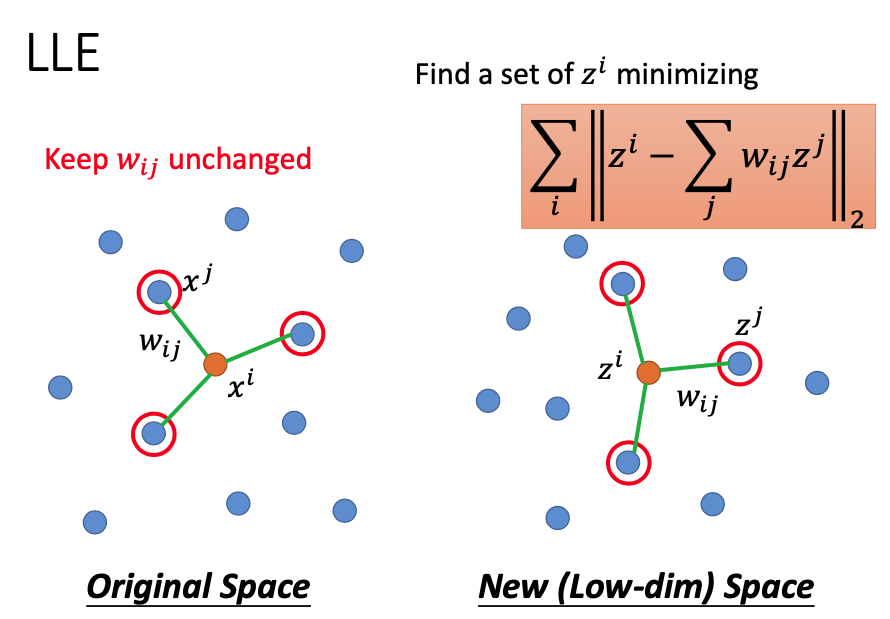
- 在找到
wij之后,固定wij,然后通过上式找到对应的zj得到降维后的点。 - 需要注意的是在这里对于整个降维过程并没有一个显示的表达,假如我们不知道x的具体值,只知道
wij是可以进行操作的,另外还有一点需要注意的是,在邻域里选择几个xj点也是需要实验才能得到的一个超参数。
- K的值是选择的邻域点个数,如上图,当选择的邻域点数过少时,降维效果并不好,可能时因为无法表达点之间的关系;
- 当邻域的点数过多时降维效果也不好,主要时因为这个方法的假设时基于局部线性假设,当选择邻域过大时,很有可能不满足局部线性的假设。
拉普拉斯特征映射(Laplacian Eigenmaps)
- 这是一种基于图的方法,首先根据数据点之间的相似性建立一个图,比如说相似性大于某个值就连接在一起,小于某个值就不连接。这时候如下图所示:
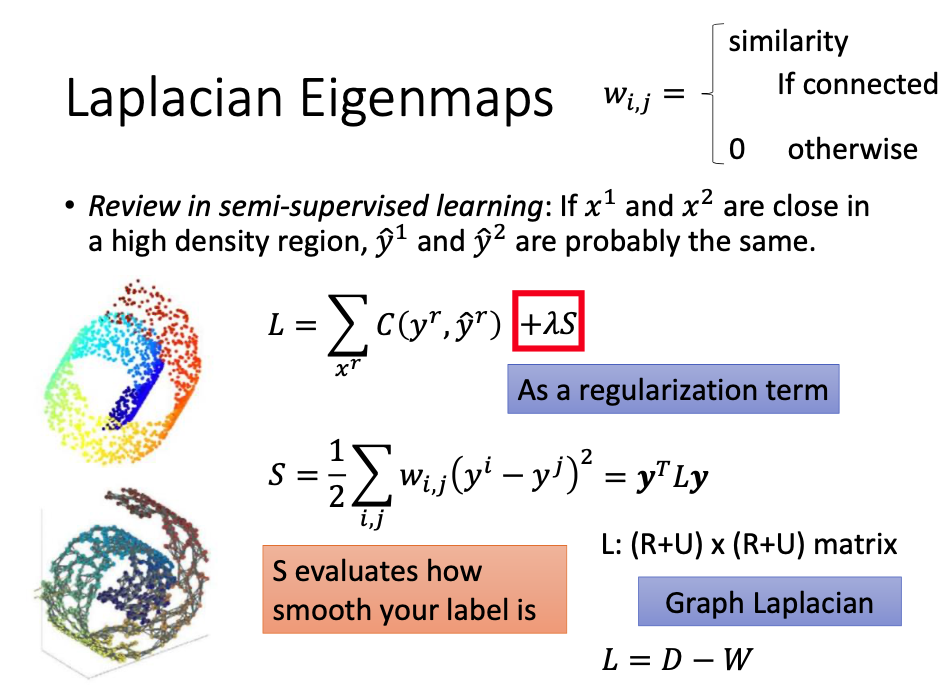
- 这个时候两个点之间的距离就可以根据图上的连接来近似。
- 这里使用有标签数据和无标签数据,其中无标签的数据的那一项更像是正则项,它刻画了标签到底有多平滑。将它应用到我们这里:
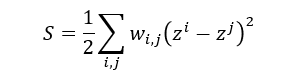
- 但是仅仅有这个表达式是不够的,因为我们只需要将所有的z都集中在同一个点,就可以达到最小值,所以还需要对这个等式添加约束:

t分布随机邻域嵌入(T-distributed Stochastic Neighbor Embedding,t-SNE)
- 上面的方法确实可以对高维非线性数据进行降维,但是它们只强调了要将相似数据放在一起,并没有强调将不相关的数据分开,所以常常会出现如下现象:
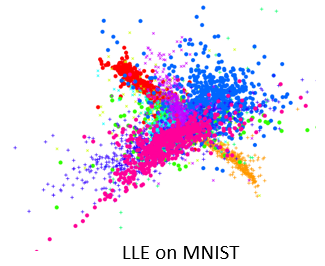
- 可以看到,相似的数据已经聚集在一起了,但是不同的数据也聚在一起,所以性能有局限性,这个时候就需要t-SNE了。
- 具体的做法如下:
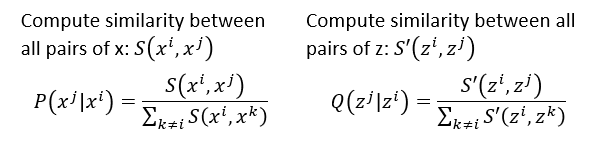
- 对于降维之前的数据,计算两点之间的相似度,并将相似度进行归一化,对于降维之后数据点也是一样的。之后通过将两个之间的KL散度最小化得到降维之后的点向量。
- 这里的相似度计算方法主要根据下面这种方式:
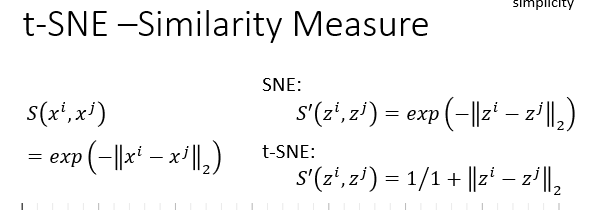
- 其中原高维数据的相似性人根据RBF函数进行计算,这种距离的计算方式可以保证距离比较远的点之间相似性可以快速下降;
- 在介绍t-SNE的相似性计算方法之前首先介绍SNE相似性的计算方法。SNE的相似性计算方法与之前的高维数据间的相似性的计算方法相同,但是t-SNE改用了下面的T分布的一种表达式,将两种计算相似性的方法曲线进行比较,我们可以知道,对于距离比较近的数据之间,它们经过计算相似性之后任保持着较为相近的距离,但是距离较远的点会变得更远,所以在保证将相似性的点放在一起的同时将不相同的点区分的较好,实验结果如下图所示:

从上图可以看到不同数据之间区分的很开。
注意很少直接对高维数据进行t-SNE降维,因为计算高维数据之前,你的相似性是十分难确定的,因此首先利用常用的线性降维方法降维进行降维(如PCA),之后再利用t-SNE进行降维。
