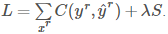介绍

  • 什么是半监督学习？既有有标记数据 xr，又有无标记数据 xu，一般无标记数据的数量远大于有标记数据。半监督学习又可以分为两种：
    • **Transductive learning:**无标记数据就是Testing data.
    • **Inductive learning:**无标记数据不是 testing data，假设在训练时不知道 testing set.
  • 为什么要用半监督学习（Semi-supervised learning）？
    • 因为收集数据比较容易，但是收集label数据的代价却很昂贵。

      半监督学习下的 generative model

  • 为了更直观的了解半监督学习下的生成模型，我们先介绍一下全监督学习下的生成模型，好让大家有个对比。

全监督学习下的生成模型

  • 首先，估计 prior probability P(Ci)，再估计出每一类有标记数据的分布 P(x|Ci)，假设数据的分布为共用协方差矩阵的高斯分布，因此只需要估计出就行，之后就可以估计某个数据属于某一类的概率了，计算公式如下：

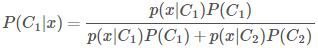
半监督学习下的生成模型

  • 前面部分与监督学习的操作一样，先使用有监督的数据估计出 P(Ci)、μi 和 Σ，接下来使用未标记的数据 xu 来对这些参数重新估计，以二分类问题为例，估计过程主要分为如下两个步骤：
    • 初始化 θ={P(C1),P(C2),μ1,μ2,Σ}，（可以随机初始化，也可以根据已有的标记数据估计出来）。
    • step1：根据初始化的参数计算无标记数据的后验概率Pθ(C1|xu) 。
    • step2：更新模型参数：

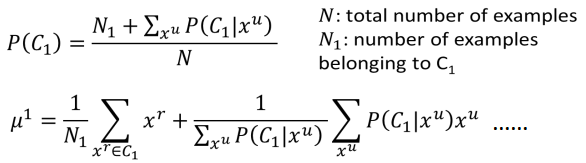
  • 接着再返回step1，直到参数收敛为止。
  • 其实上面这个过程，我们用到了再机器学习领域一个超级NB的算法的思想，它就是EM(Expectation-maximization),step1就是 E，step2就是 M. 这样反复下去，在最终一定会收敛.

半监督学习之低密度分离假设（Low-density Separation）

  • 在用这个假设的时候，需要假设有一个很明显的区域(Low-density),能够把数据分开。

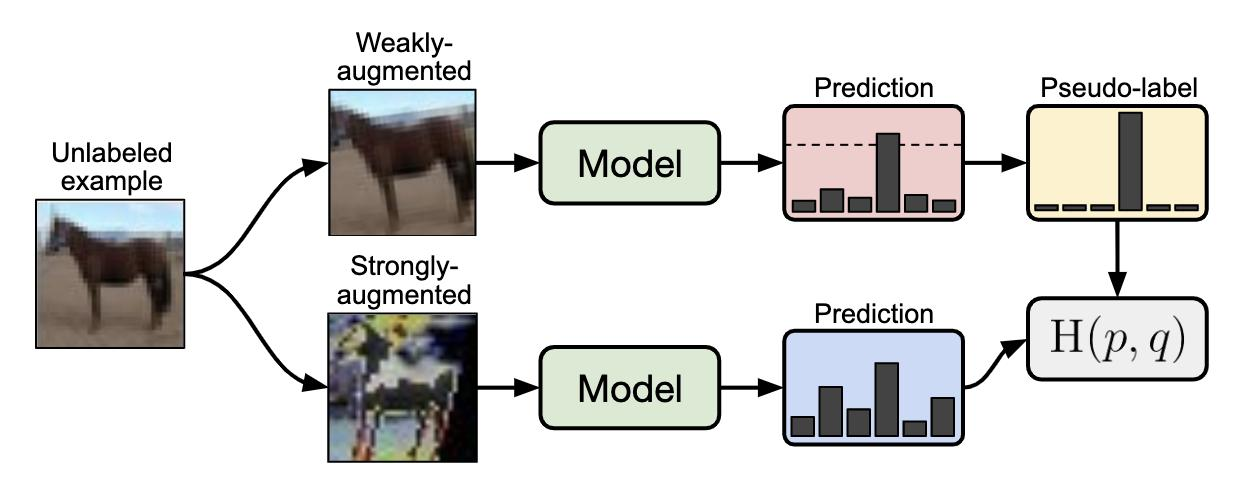
    Self-training

  • 先对有标记数据训练出一个模型f*,这个可以模型可以用任何方法训练。
  • 用这个 f∗ 来预测无标记的数据，预测出的就叫 pseudo label.
  • 接下来，就用无标记数据中拿出一部分数据，放到有标记数据中，怎么选出这部分是自己定的，也可以对每一个数据提供一个权重。新加入了这些数据之后，就可以再重新训练一个 f∗，往复进行。
  • 这招用在 regression 中，是没有用的，因为用预测出来的数字重新用来做训练，并不会影响模型的参数。
  • 在做 self-training 时，其实就是把某个未标记数据指定一个分类，而在 generative model 中，其实就是把未标记数据对应于各个分类的概率计算出来。

基于熵的正则化(Entropy-based Regularization)

  • 假如未标记数据数据 xu 经过某一组参数估计后属于某一类的概率如下：

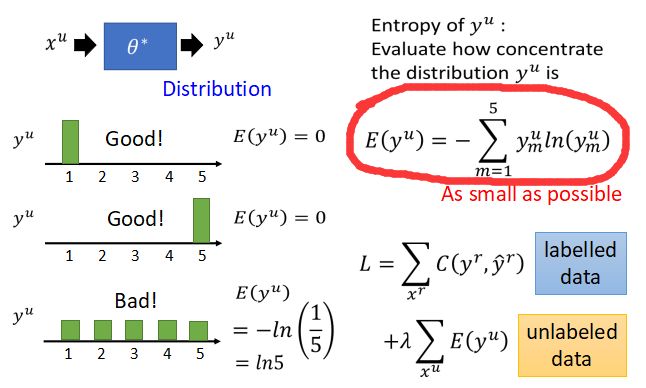
  • 又边红圈中的公式为熵的计算公式。由上图可知 xu 属于某一类的概率越大，熵的值E就越小，因此重新定义损失函数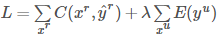，其中E(yu)可以微分，我们可以直接用梯度下降法来求解。

Semi-supervised SVM

  • 将未标记数据穷举所有的分法，然后对每一种分法都进行 SVM，具有最大的间隔和最小误差的那一种。
    但是，如果有 10000 个未标记数据，那么就会有 210000 种分法来穷举，Transductive Inference for Text Classification using Support Vector Machines 中提出的解决办法是，每次只改一个数据，看一下能否让间距变大，变大了就改。

平滑假设(smoothness assumption)

  • 做出如下假设：
    • x的分布不均匀，在有些地方集中，有些地方分散，若x1和x2在一个high density region内很接近，那么 y^1 就与 y^2 相同，那么什么是high density region呢？请看下图：

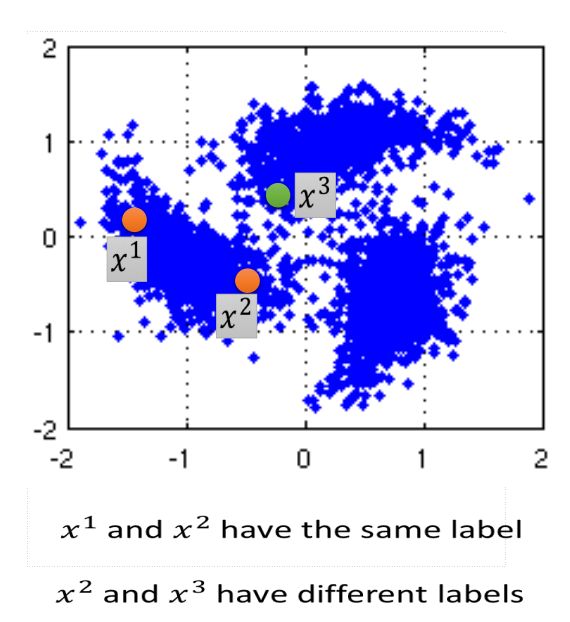
  • 在图中，虽然x2与x3比较接近，但是x1与x2在同一块high density region，所以 y^1 与 y^2 相同,y^2 与 y32 不相同。

基于图的方法(Graph-based Approach)

  • 首先需要定义相似度，一般可以用 Gaussian Radial Basis Function (RBF) 来定义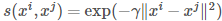：，这个函数可以让相似度随着距离的增加而迅速减小。
  • 定义完相似度之后，就可以逐渐把数据点之间相连的边加上去，加边可以用 kNN 或者 e-Neighborhood 的方法来做。然后设置边的权重，和 s(xi,xj) 成比例。
  • 然后，定义在图上的标记的平滑因子(smoothness)S: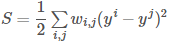，该式可以写成 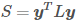，y 是 R+U 维的向量（所有的有标记和无标记数据），L=D−W，W 是所有数据之间两两的连接权重，D 是对角矩阵，对角线上的值是每个数据点所有的连接的权重之和。之后，就可以定义出 loss function: