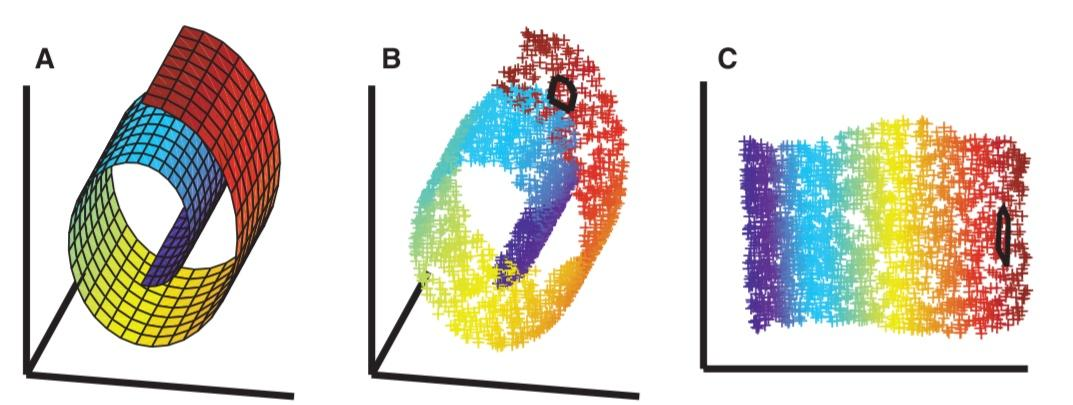
介绍
- 本节主要介绍了两种线性降维的方法:Cluster和PCA,并从两个角度解释了PCA。
聚类(Cluster)
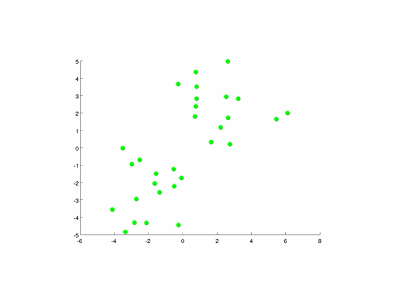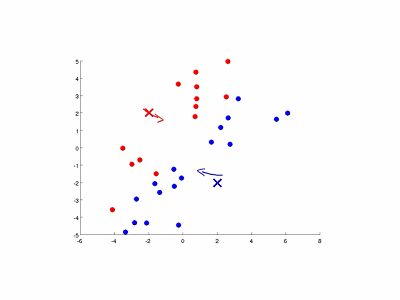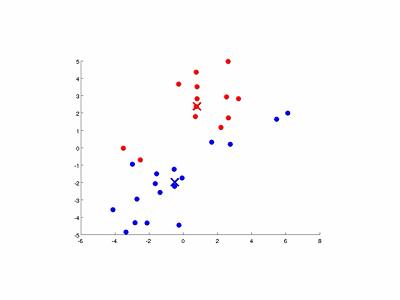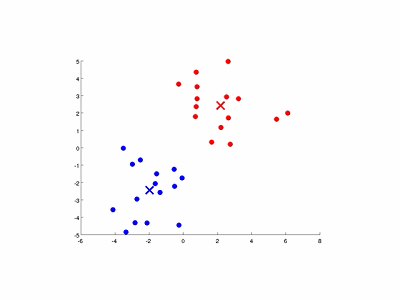
- 随机初始化K个样本(点),称之为簇中心(cluster centroids);
- 簇分配: 对于所有的样本,将其分配给离它最近的簇中心;
- 移动簇中心:对于每一个簇,计算属于该簇的所有样本的平均值,移动簇中心到平均值处;
- 重复步骤2和3,直到找到我们想要的簇.
- 如下图演示了特征量个数和簇数均为2的情况:
分层凝聚聚类(Hierarchical Agglomerative Clustering,HAC)原理
- 顾名思义就是要一层一层地进行聚类,可以从下而上地把小的cluster合并聚集,也可以从上而下地将大的cluster进行分割。似乎一般用得比较多的是从下而上地聚集,因此这里我就只介绍这一种。
- 所谓从下而上地合并cluster,具体而言,就是每次找到距离最短的两个cluster,然后进行合并成一个大的cluster,直到全部合并为一个cluster。整个过程就是建立一个树结构,类似于下图。
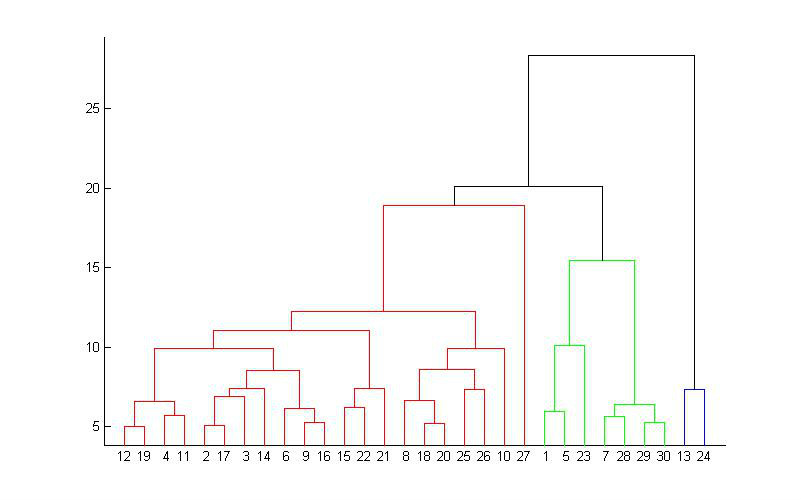
- 层次聚类最大的优点,就是它一次性地得到了整个聚类的过程,只要得到了上面那样的聚类树,想要分多少个cluster都可以直接根据树结构来得到结果,改变cluster数目不需要再次计算数据点的归属。层次聚类的缺点是计算量比较大,因为要每次都要计算多个cluster内所有数据点的两两距离。另外,由于层次聚类使用的是贪心算法,得到的显然只是局域最优,不一定就是全局最优,这可以通过加入随机效应解决,这就是另外的问题了。
主成分分析(Principle Component Analysis,PCA)
- PCA降维原理可以从两个角度来考虑:
- 基于最大方差原理,样本点在这个超平面上的投影尽可能分开。
- 基于最小化误差原理,样本点到这个超平面距离都足够近。
基于最大方差原理
- 需要找到一个投影矩阵W,使得x在W上的投影方差尽可能大,其中W是由多个向量组成,其中W是由多个向量组成(w1,w2,w3…),希望x在w1上的投影的方差最大,w2上的投影的方差其次…..依次类推。
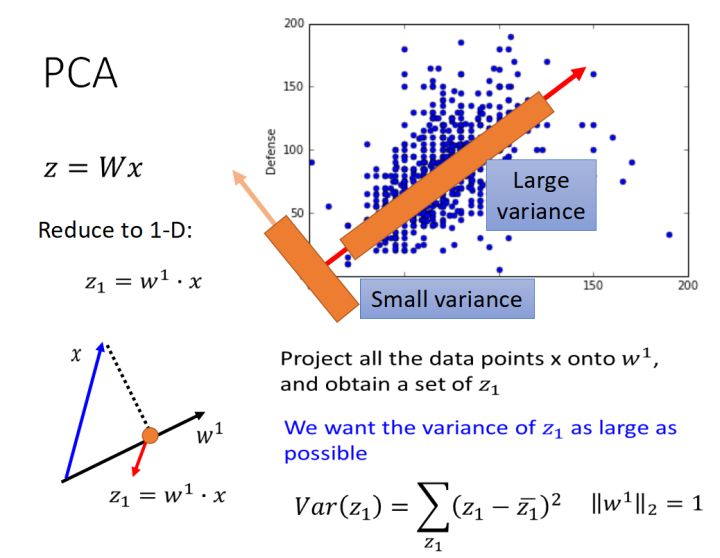
- 并且,W是一个单位正交矩阵,即(w1,w2,w3,…)相互正交,且都是单位向量。

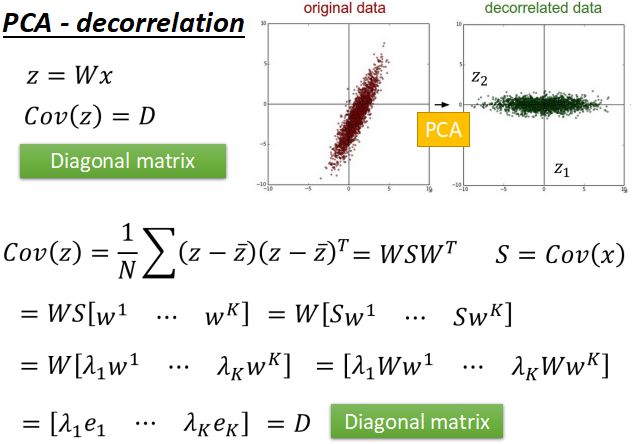
- PCA达到的效果就是decorrelation(去关联),所以最后投影之后得到z的协方差矩阵D是对角矩阵;
- 投影矩阵W是单位正交矩阵。
- W就是x协方差矩阵S的特征向量。
基于最小化误差原理
- 基本思想:将
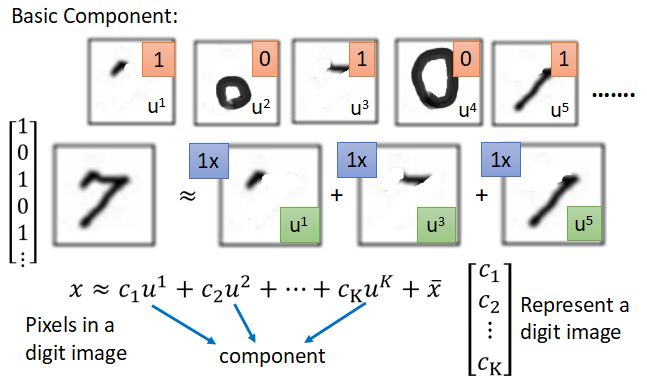
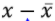 近似看成由多个u组成,求解最小化他们之间的error时的系数c和分量u。
近似看成由多个u组成,求解最小化他们之间的error时的系数c和分量u。 - 其中向量(u1,u2,u3…)表示一个
Basic component,如下图:

- 为了求解c和u(component),可以将X做奇异值分解SVD,用分解后的U代替u,ΣxV代替系数c
其中U就是XXT的特征向量 - 有时候只选取特征值比较大的
component。 - PCA相当于只含一层hidden layer的网络。

PCA与LDA(Linear Discriminant Analysis)的比较
- PCA是无监督的,LDA是有监督的;
- PCA基本思想是方差最大,LDA基本思想是让不同类别分的尽可能开;
- PCA和LDA都是线性映射;
- 对于结构比较复杂的降维,只能采用非线性流行学习比如局部线性嵌入(Locally Linear Embedding,LLE)等方法.
PCA和非负矩阵分解(Non-negative Matrix Factorization,NMF)比较
- NMF分解之后的component的系数都是正的,就拿image来说,也就是说分解之后的component像是原始image的一部分;
- 而PCA的系数可正可负,涉及到component的“加加减减” .