分割精度性能度量

介绍

• 为了能对提出的方法的性能进行定量的评估。本文采用了和2007年医学影像计算与计算机辅助介入国际会议（MICCAI）医学图像分割竞赛[21]相同的两个基于体积的度量指标体积重叠率（Dice Similarity Coefficient，Dice）和基于表面距离的度量指标平均对称表面距离（Average Symmetric Surface Distance，ASD）来对分割结果A与手动分割金标准B进行比较。其中体积重叠率（Dice）与平均对称表面距离（ASD）的定义如下：
• （1）体积重叠率（Dice Similarity Coefficient，Dice）：在定义体积重叠率之前需要先定义分割结果A和金标准B的体积重叠率系数，也称Jaccard系数( Jaccard Index，JI )[22]:

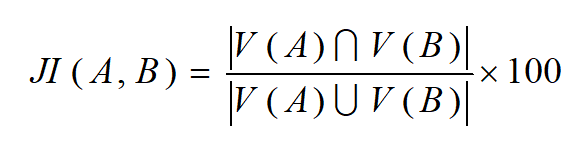
• 其中，V(A)表示分割结果A的体素集合、V(B)表示金标准B的体素集合。相应的，体积重叠率（Dice）就可以定义为：

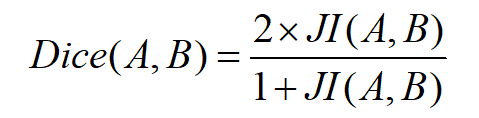
• （2）平均对称表面距离（Average Symmetric Surface Distance，ASD）：它是基于表面距离的度量指标。定义为分割结果A的表面体素S(A)与金标准B的表面体素S(B)之间的平均距离：

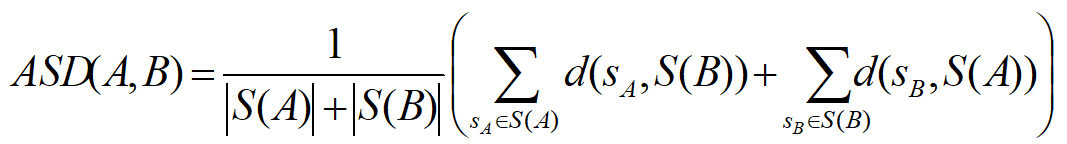
• 其中，d(v,S(X))定义为体素V到分割结果X表面体素的最小欧式距离：

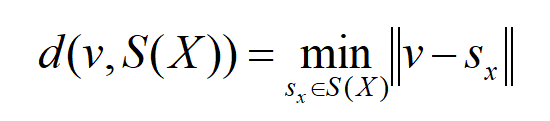
• 这两个基于体积的度量指标体积重叠率（Dice）和基于表面距离的度量指标平均对称表面距离（ASD）的单位分别为%和mm，对于体积重叠率（Dice）来说，值越大表示分割结果越精确，对于平均对称表面距离（ASD）来说，值越小说明分割结果越精确。

算法实现

• 计算体积重叠率的时候，先计算分割结果和金标准的非零体素的总个数volume1+volume2，再计算体素重叠的个数intersection，用intersection/（volume1+volume2）得到JI，再用Dice计算公式得到Dice。

• 部分代码如下：

  // Tanimoto overlap metric
    unsigned long volume1=0, volume2=0, intersection=0;
    IteratorType resIt( resultImage, resRegion ), valIt( validationImage, valRegion );
    for ( resIt.GoToBegin(), valIt.GoToBegin(); !resIt.IsAtEnd(); ++resIt, ++valIt ) {
  	if (resIt.Get()!=0) {
  	  volume1++;
  	  if (valIt.Get()!=0) {
  		volume2++;
  		intersection++;
  	  }
  	}
  	else {
  	  if (valIt.Get()!=0) volume2++;
  	}
    }
    double tanimotoVal = 100.0 * (double)(intersection) / ((double)(volume1+volume2-intersection));
    double tanimotoError = 100.0 - tanimotoVal;
   //求dice
    double jiError = (100.0 - tanimotoError)/100.0;
    double diceError = 2 * jiError/(1 + jiError) * 100;
  

• 计算平均对称表面距离ASD的时候，需要先计算分割结果和金标准元素在同一个坐标系里面的全球坐标，再利用ANNkd_tree类求平均表面对称距离。

• 部分代码如下：

   ANNpointArray borderPts2 = annAllocPts( numBorderPts2, 3 );
   numBorderPts2 = 0;
  for ( it2.GoToBegin(); !it2.IsAtEnd(); ++it2 ) {
  if (it2.Get() != 0) {
    validationImage->TransformIndexToPhysicalPoint( it2.GetIndex(), pnt );   //将像素数组中的Index转换为物理空间中的坐标。
    for (int d=0; d<3; d++) borderPts2[numBorderPts2][d] = pnt[d];
    numBorderPts2++;
   }
   }
   ANNkd_tree *borderTree2 = new ANNkd_tree( borderPts2, numBorderPts2, 3 );
   ANNidxArray  nnIdx = new ANNidx[1];
   ANNdistArray dists = new ANNdist[1];
   
  for(unsigned int idx1=0; idx1<numBorderPts1; idx1++) {
  borderTree2->annkSearch( borderPts1[idx1], 1, nnIdx, dists);
  avgSqrDistance += dists[0];
  double d = sqrt( dists[0] ); //分割结果到金标准的最小欧式距离
  avgDistance += d;
   if (d>maxDistance) maxDistance = d;
   }