介绍
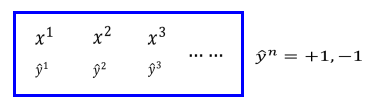
- 其中x表示数据向量,y表示数据标签,标签分为两类,即+1和-1.在这里去模型函数为:

- 所以分类用的损失函数为:
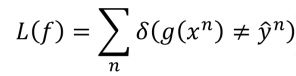
- 其中定义当计算出的函数值于标签不相等的时候取1,相等的时候取0,但是这样得到的函数有一点不好,它无法进行微分,即无法进行梯度下降。所以我们采用了另外一种函数作为损失函数,即:
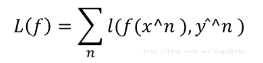
对各种损失函数的讨论
- 在下面我们将讨论各种损失函数的特性,如下图所示:
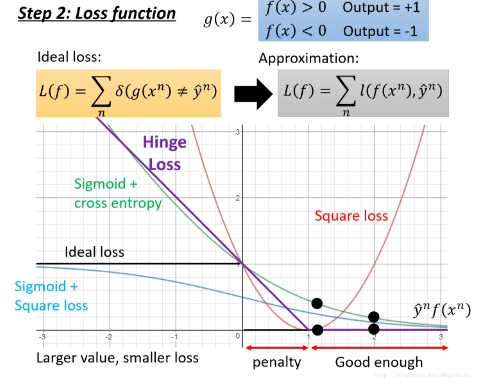
- 在上图中,横坐标是
,如果预测的符号于原始标签的符号是相同的,那么它们的损失值为0,如果符号相反则损失值为1,其中黑色的线是理想损失函数曲线,但是可以明显的看到这是一个不可微分的函数,所以我们使用了近似损失函数进行代替,这个近似损失函数可以由多种选择,下面将对每一种可能的选择进行讨论:
- 其中红色曲线是二次函数曲线,其损失函数的表达式为:
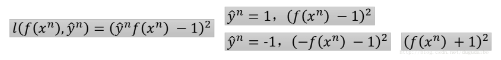
- 我们可以看到当数据的标签值是 +1 的时候,预测值为 +1 可以达到最小的损失;当标签值为 -1 的时候,预测值为 -1 可以达到最小的损失。所以当 y^nf(xn)=1 的时候取到最小的损失函数值,但是在后面这个函数就是不合理的,因为随着预测值逐渐变大,损失函数的取值居然越来越大,这明显是不合理的。
- 接下来我们考虑使用
sigmoid+square loss作为损失函数,其函数曲线是蓝色的那一条,具体的损失函数如下:
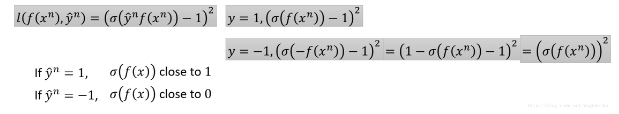
- 画出损失函数曲线如上图所示,这个方法的效果并没有使用交叉熵的效果好,具体原因如下:
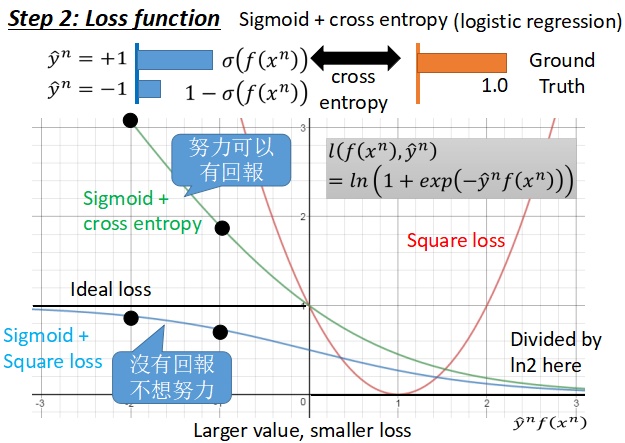
从表达式可以看出,如果
,那么整体的函数值将趋近于 ln1=0,如果
,那么整体的函数值将趋近于 ∞,所以函数曲线如上图。这个函数曲线是合理的,因为随着 y^nf(xn) 的增加函数值会逐渐下降。对比 sigmoid + square loos 作为损失函数的方法,我们可以看到,当自变量(横坐标对应的值)取到负无穷的时候, sigmoid + cross entropy 会有很大的梯度值,而 sigmoid + square loos 的梯度值几乎为0,也就是说,前者在梯度下降的过程中,主要努力就会得到回报,而后者没有回报,所以也很有可能不想努力。另一点,在这里我们将交叉熵的函数值除以了 ln2,主要目的是希望可以得到理想损失函数的一个上界。
最后我们来考虑折页损失函数(
Hinge Loss),具体表达式以及函数曲线如下图所示:

如上的损失函数,我们可以看到,对于一个正例,如果 f(x)>1,那么便得到了一个完美的分类结果,如果是反例的话,如果 f(x)<−1,那么便得到了一个完美的分类结果。所以x 不用太大,因为大了函数值也是相同的。观察函数曲线可以知道,当
的时候,就已经够好了,但是它们同向却在
penalty认为实际上还不够好,虽然可以正确分类了,但是损失函数仍然或让自变量向右移动变得更好,这个区间也就是所谓的边界(margin)。其中损失函数中取 1 的原始,它可以得到理想损失函数的一个紧致的上界。如果我们对比交叉熵函数和折页损失函数的话,它们最大的区别在于对待已经正确分类的例子的态度。如果将图中的黑点从1 的位置移动到 2 的位置,我们可以看到交叉熵损失函数的函数值会继续下降,也就是说它在已经得到好的结果之后还希望得到更好的结果;但是折页函数是一种及格就好的函数,当大于margin的时候就好了。在实际的使用中,折页函数略优于交叉熵损失函数,就是说没有领先的很多。但是折页函数更能够顾全全局,当进行多分类的时候得到的效果会更好。
线性SVM分类器
- 线性的SVM的步骤主要如下图所示分为三部:

第一部分是目标函数,这里使用如上图所示的目标函数,它可以表示为两个向量之间的点积运算,进而可以表示为权重的转置与输入 x 的相乘。
第二步,构建损失函数,这里使用的是折页损失函数和 L2 的正则项,因为前面的损失函数明显是一个凸函数,后面的正则化项也明显是一个凸函数,所以这些的组合也是一个凸函数;
这样在第三步就可以使用梯度下降的方法更新参数。有的人可能会想,这个函数是分段线性的可以使用梯度下降嘛,可以的。想想之前的RElu,也是这样的啊,同样可以使用梯度下降的方法进行训练。
在这里我们可以看到,实际上逻辑回归和线性的 SVM 之间的区别就在于 损失函数的不同。另一方面,通过第一步我们可以看出,实际上SVM与神经网络之间是相通的,所以在2013年的ICML中有一篇文章是“Deep Learning Using Linear Support Vector Machines”。
使用梯度下降训练SVM
- 首先我们将损失函数中折页损失函数取出,并判断下面两个等式是否相等:
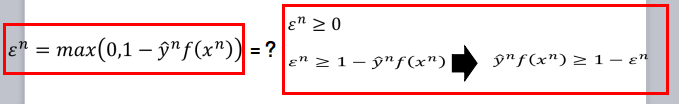
- 实际上仅仅考虑这两个等式,他们之间是不相等的,但是同时考虑最小化如下的损失函数的话,两者就是相同的了:

- 这个时候我们用 ϵ 代替原来的折页损失函数,这里 ϵ 满足之前红色框框内的两个不等式,所以在这里我们认为他是松弛变量,而这样的问题可以使用二次规划的方法进行求解。
核方法
对偶表示
- 最后分类函数的权重实际上是输入数据的线性组合,如下图所示
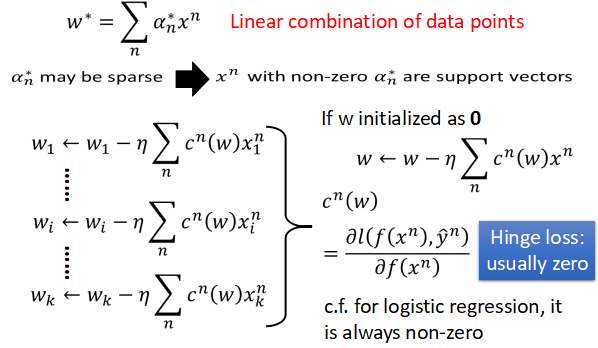
- 造成这种结果的原始,实际上可以通过之前所讲的利用梯度下降的方法更新参数的角度进行考虑。如上图所示,我们将所有的权重更新的过程合并成一个向量,其中的折页损失函数的导数记为 cn(w),他的具体表达式也如上图所示。如果我们将权重的初始值设为0 的话,那么参数 w 实际上就是输入数据的线性组合,另外因为对于折页损失函数来讲,它里面有很多零的值,所以系数 α 中有很多的0,这样权重实际上是输入数据的稀疏组合,其中稀疏不为零所对应的数据点称为支持向量。这样的结果导致模型的鲁棒性更强,即使有离群值的点或者不合理的点,只要不选取它们作为支持向量,那么对于分类结果的影响并不大。
- 由于在上面的部分已经证明了,SVM的权重实际上是通过输入点的线性组合得到,因此它可以表示为如下的形式:
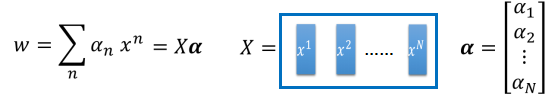
- 这里是将原来的求和转变为了向量相乘的形式,这个表达方式在机器学习中是常常使用的。在得到了的权重的对偶表达方式之后,第一步是进行变量替代,如下图所示
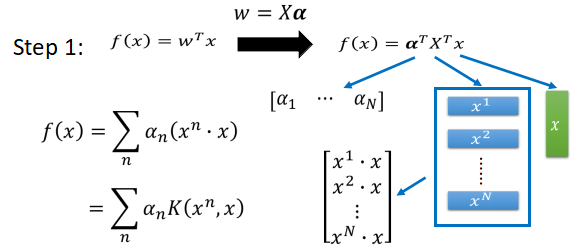
- 将 w 带入之后可以看到 f(x) 主要这三部分组成,第一部分是系数 α ,他是一个行向量,一共有 N 列,后面的两项可以使用矩阵乘法的结合律,得到一个列向量,一共有 N 行。所以 f(x) 可以表示为上图那种形式,将其中的
可以表示为
,我们将
K称为核方法。 - 如下图所示,经目标函数表达为系数与
的线性组合之后,接下来的任务就是最小化损失函数:
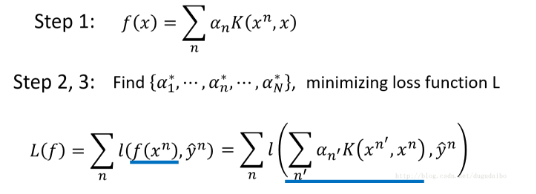
- 其中需要注意的是,虽然后一项中有 n 还有 n′ ,但是这两个的求和范围是相同的,只不过先对 n′ 进行求和运算再对 n 进行求和运算。在这里我们不是真的需要知道向量 xn,只需要知道向量 xn 与 xn′ 的内部关系即可。这种方法就叫做核技巧(Kernel Trick)。
核技巧(Kernel Trick)
- 当我们将原来的数据点映射到高维空间的时候,这个时候使用核技巧往往是十分有用的,如下图所示:
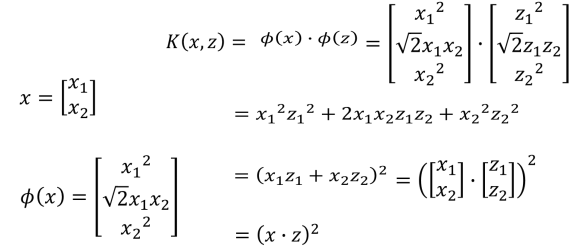
- 如上图中我们将 x 映射到 Φ(x),这个时候我们计算转化到高维再做点积,通过化简可以知道这个过程等价于先对原始数据进行点积,之后再平方。这种方式主要在输入数据是高维数据的时候可以减少大量的计算量,如下图所示:
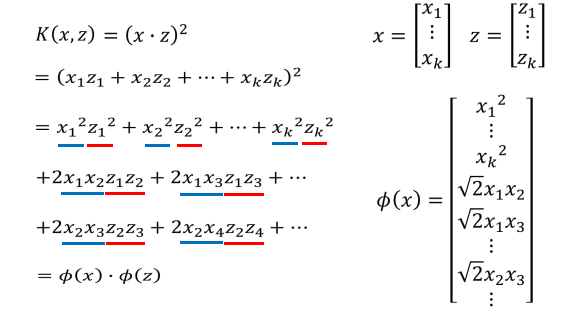
如果首先做高维映射的话,需要进行
乘法得到高维数据的点,之后再让高维的点之间进行点积,一共需要
次乘法。但是如果首先进行内积运算在进行平方运算的话,需要计算 k+1 次乘法。这个计算量明显要小很多。所以核技巧的主要作用是减少计算量。
下面再以径向基核(Radial Basis Function Kernel)为例进行介绍

我们可以看到如果将径向基函数用泰勒公式展开的话,我们可以看到是无穷多项的求和,所以是没有办法通过先向高维映射,之后在进行点积的方法求解的。另外通过上面的过程我们也可以了解到,实际上RBF(Radial Basis Function)核实际上是一种在无穷维上的分类器,虽然效果比较好,但是也十分容易过拟合。
接着我们以 Sigmoid 核为例进行介绍
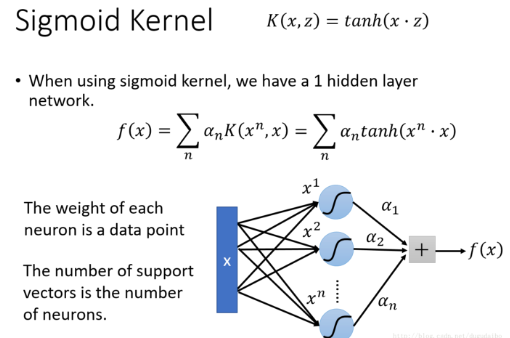
- 我们实际上可以看到 f(x) 的计算过程可以通过如下的神经网络进行计算,对于输入的数据 x ,它首先与 x1 做点积,这个过程实际上即使在计算第一个神经元的加权输入,一共有 n 个这样的神经元,它们与对应的系数相乘再相加就可以可到目标函数 f(x)。因此使用 Sigmoid 核的SVM实际上是一个只包含一个隐层,激活函数为 Sigmoid 函数的神经网络。
- 并不是所有的先对向量做点积再做其他操作都有对应的核函数,只有满足Mercer’s theory can check的才可以。
深度学习与支持向量机的关系
- 深度学习与支持向量机在原理上有很大的相关性,具体如下图所示:
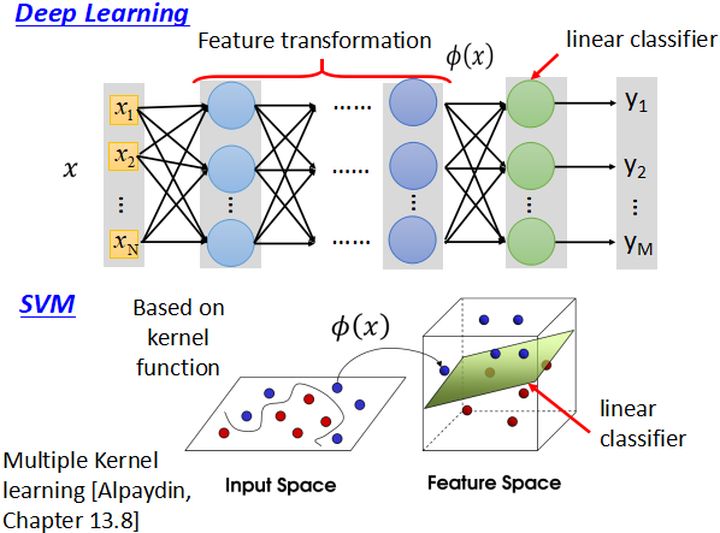
- 深度学习前面的隐层实际上是在做特征的高维映射,最后使用一个线性的分类器进行分类;
- 而SVM使用核方法对数据进行非线性映射,之后在使用线性分类器进行分类。
- 两者都是先特征映射再做分类的方法,这里实际上SVM的核方法也是可学习的,但是它们没有办法学习到深度学习那种程度。
- 当你使用多个核函数的时候,对于两个核之间的连接的权重是可以学习的,就好像之前的SVM只有一个隐层,当使用多核方法的时候就相当于有多个隐层,那么它们之间权重就是可学习的了。
